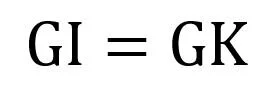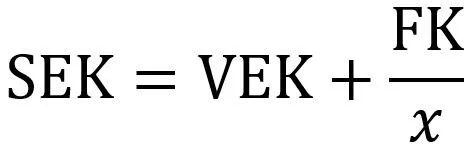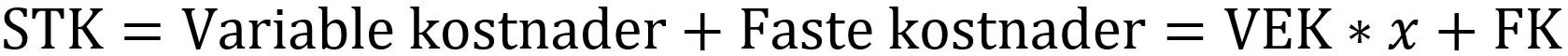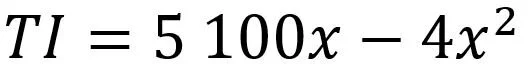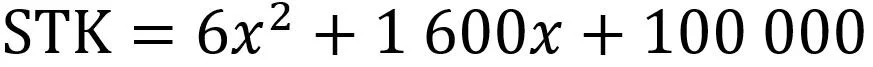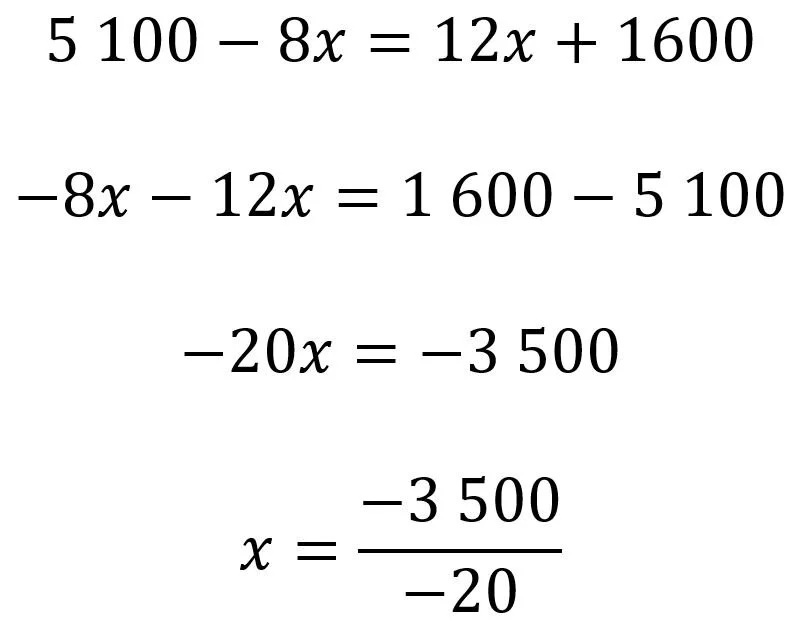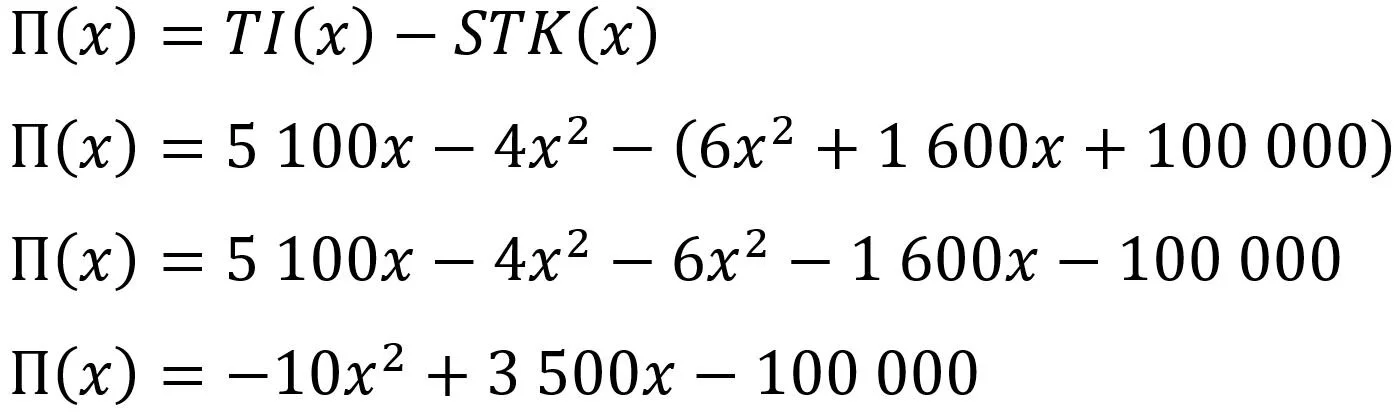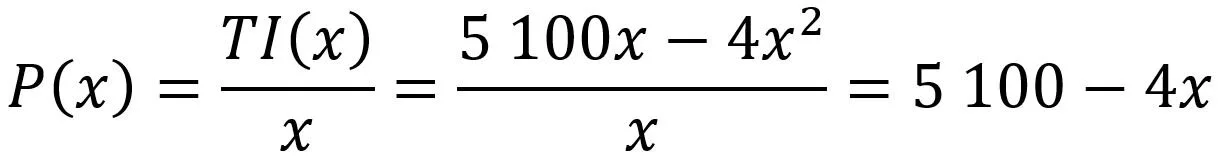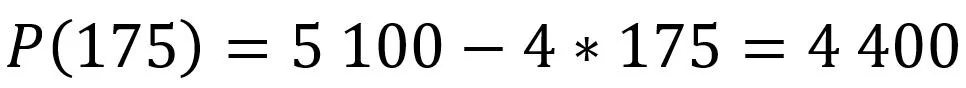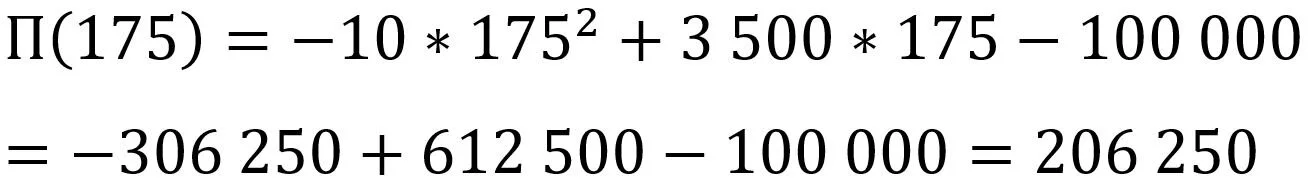Med vinningsoptimum forstår vi den mengden som gir oss maksimal profitt. Det er her vi oppnår den største fortjenesten. Dette blir også omtalt som profittmaksimering. Ofte vil vi være interesserte i å bestemme både vinningsoptimal mengde og vinningsoptimal pris. I monopolmarkeder (kjennetegnet ved at prisen kan påvirkes) henger de sammen. I et fullkomment konkurransemarked (kjennetegnet ved at prisen er gitt) kan vi ikke påvirke prisen, slik at vi bare er interesserte i å bestemme vinningsoptimal mengde. Fremgangsmåten er den samme i begge tilfellene.

Uavhengig av fremgangsmåte ønsker vi å bestemme det punktet hvor grenseinntekten (den marginale inntekten; inntekten vi oppnår ved å selge én enhet til) er lik grensekostnaden (den marginale kostnaden; kostnaden vi må tåle ved å produsere én enhet til):

Generell likning for å bestemme vinningsoptimum. Grenseinntekt settes lik grensekostnad.

Noen henviser til dette som det punktet hvor differanse enhetsinntekt (ofte forkortet til DEI, som tilsvarer grenseinntekt) er lik differanse enhetskostnad (ofte forkortet til DEK, som tilsvarer grensekostnad). Betegnelsen er ikke relevant, da de forskjellige begrepene medfører den samme beregningen.

Grenseinntekten (evt. differanse enhetsinntekt) er definert som den deriverte av inntektsfunksjonen. Inntektsfunksjonen er totalinntekten, som noen ganger forkortes til TI (for Total Inntekt). Totalinntekten er definert som salgspris per enhet ganger antall solgte enheter.

Grensekostnaden (evt. differanse enhetskostnad) er definert som den deriverte av kostnadsfunksjonen. Kostnadsfunksjonen er av og til betegnet sum totale kostnader, og forkortet STI. Dette er kostnadene ved å produsere alle enheter.

Generelt sett kan vi si at det er to måter å komme frem til en løsning. For det første kan vi benytte en matematisk (regneteknisk) løsning. For det andre kan vi benytte en grafisk tilnærming.

Problemet med den grafiske tilnærmingen er at det ofte vil være vanskelig å bestemme en konkret løsning. Hvor enkelt vil det eksempelvis være å skille mellom 273 og 274 enheter? Generelt er derfor min preferanse, og anbefaling, å benytte den regnetekniske tilnærmingen. Den grafiske løsningen kan være aktuell dersom vi har flere knappe faktorer og skal bestemme optimal produksjon, basert på de begrensede ressursene vi har tilgjengelig. Da får vi som regel flere likninger som sammen setter begrensninger. En grafisk fremstilling vil da være nyttig til å bestemme hvor mulighetsområdet ligger.

Den matematiske fremgangsmåten baserer seg på å bestemme grenseinntekten og grensekostnaden, og deretter løse for sammenhengen. Det er noen beregninger det kan være lurt å ha kjennskap til før vi ser på et eksempel. De aktuelle begrepene og tilhørende forkortelser er: 1) Salgspris (P, for pris), 2) Salgsinntekt (TI, for totalinntekt), 3) Variable enhetskostnader (VEK), 4) Sum enhetskostnad (SEK), og 5) Sum totale kostnader (STK; må ikke forveksles med forkortelsen for stykk [stk.]).

Prisen vil enten være gitt i markedet fordi vi opererer i et frikonkurransemarked. Da bestemmer markedet prisen, som enhver tilbyder må akseptere. Dette har lite feste i realiteten, men er en viktig forenkling i teorien. Hvordan skal vi for eksempel justere prisen for at vi har en annen farge enn konkurrentene? Dersom prisen ikke er gitt, er denne definert som totalinntekten dividert på antall solgte enheter.

Salgsinntekten (eller totalinntekten, TI) er produktet av salgspris pr. enhet og antall solgte enheter. Dersom vi har en markedspris på 100 og vi selger 20 enheter, får vi en salgsinntekt – eller totalinntekt (TI) – på kr. 2 000 (100 * 20).

Følgelig kan vi vise denne generelle sammenhengen:

Likning for å bestemme pris, når totalinntekt (TI) og mengde (x) er gitt. Alternativt kan totalinntekten bestemmes som produktet av enhetsprisen og solgt mengde.

Variable enhetskostnader (VEK) er de variable kostnadene per enhet. Vi fordeler da alle de variable kostnadene på antall produserte (evt. solgte) enheter. Ofte vil vi komme frem til dette tallet den «andre veien», det vil si ved å ta utgangspunkt i en kalkyle.

Sum enhetskostnader (SEK) er summen av alle kostnadene som går med på å produsere én enhet. Dette vil si de variable enhetskostnadene (VEK) og de faste kostnadene pr. enhet. Vi finner de faste kostnadene (ofte forkortet til FK) pr. enhet ved å dividere de faste kostnadene på produserte enheter, altså:

Likning for å bestemme sum enhetskostnader. Likningen kommer frem til kostnaden ved å produsere én enhet. Dette er summen av de variable kostnadene som går med på å fremstille produktet, samt de faste kostnadene fordelt på den totale produksjonsmeng… — Likning for å bestemme sum enhetskostnader. Likningen kommer frem til kostnaden ved å produsere én enhet. Dette er summen av de variable kostnadene som går med på å fremstille produktet, samt de faste kostnadene fordelt på den totale produksjonsmengden.

Alternativt kan vi finne sum enhetskostnader ved å dividere alle kostnader på produsert mengde. Vi unngår normalt denne fremgangsmåten fordi ikke absolutt alle kostnader skal være med i beregningen. Det er naturligvis mulig å ta utgangspunkt i resultatregnskapet og trekke ut de postene som ikke skal være med i beregningen.

Til sist har vi sum totale kostnader (STK). Dette er summen av de variable kostnadene og de faste kostnadene. Vi kan dermed illustrere dette som følger:

Likning for fastsettelse av totalkostnader, sum totale kostnader (STK). Sum totale kostnader består av de variable kostnadene og de faste kostnadene. Generelt kan vi si at dette er de variable enhetskostnadene ganger antall produserte enheter, med t… — Likning for fastsettelse av totalkostnader, sum totale kostnader (STK). Sum totale kostnader består av de variable kostnadene og de faste kostnadene. Generelt kan vi si at dette er de variable enhetskostnadene ganger antall produserte enheter, med tillegg av de faste kostnadene.

Eksempel

En bedrift selger et spesialisert kjemisk produkt. Selskapet har monopol på det norske markedet, og ber om hjelp til å finne den mest optimale tilpasningen i dette markedet. Bedriften har registrert følgende sammenheng mellom inntekt og solgt mengde:

Hvor TI er total inntekt og x er mengde (antall enheter).

Vi får videre oppgitt at det er identifisert følgende sammenheng mellom produsert mengde og kostnader:

Hvor funksjonen beskriver totale kostnader avhengig av produsert mengde (x).

Hvilken mengde og hvilken pris gir høyest resultat ved monopolstilpasning i Norge? Hva blir resultatet ved en slik tilpasning?

Fremgangsmåte

Det er to matematiske fremgangsmåter som kan benyttes. For det første kan vi bestemme profittmaksimum ved å sette de deriverte av henholdsvis inntekts- og kostnadsfunksjonene like hverandre. For det andre kan vi bestemme profittfunksjonen og finne toppunktet til denne. Begge metodene gjennomgås – ingen av dem er mer korrekt enn den andre, da begge skal resultere i samme løsning.

Første alternativ

Vi bestemmer de deriverte av funksjonene, og kommer frem til følgende:

- Den deriverte av inntektsfunksjonen er 5 100 – 8x

- Den deriverte av kostnadsfunksjonen er 12x + 1 600

Vi setter disse like hverandre, slik at vi kommer frem til:

Bestemmelse av profittmaksimerende produksjonsmengde.

Beregningen over viser at den profittmaksimerende produksjonen er 175 enheter.

Andre alternativ

Alternativt kan vi bestemme profittfunksjonen og finne toppunktet til denne. Vi starter med å bestemme profittfunksjonen (representert ved en stor pi):

Bestemmelse av profittfunksjon. Profittfunksjonen er differansen mellom inntektene og kostnadene, her representert ved totalinntekten (TI) og totalkostnaden, eller sum totale kostnader (STK).

For å bestemme toppunktet kan vi på enkleste måte benytte formelen som gir oss denne x-verdien, . b er representert ved faktoren tilhørende leddet med den ukjente verdien opphøyet i første, altså 3 500, mens a er representert ved faktoren tilhørende leddet med den ukjente verdien opphøyet i andre, altså minus 10. Dermed kommer vi frem til følgende beregning:

Bestemmelse av ekstremalpunkt, i dette tilfellet toppunkt. Merk at det etter andre likhetstegn er gjort en beregning, slik at minustegnene eliminerer hverandre. Heller enn å fortsette med negative fortegn, “divideres disse ut”, slik at kommer frem t… — Bestemmelse av ekstremalpunkt, i dette tilfellet toppunkt. Merk at det etter andre likhetstegn er gjort en beregning, slik at minustegnene eliminerer hverandre. Heller enn å fortsette med negative fortegn, “divideres disse ut”, slik at kommer frem til et positivt uttrykk. Dette er bare mulig når både nevner og teller er negativ.

Vi ser at denne fremgangsmåten også ga oss den samme løsningen, en produksjonsmengde (eller salgsmengde) på 175 enheter.

Konklusjon

Vi har kommet frem til at den vinningsoptimale produksjons-/salgsmengden er 175 enheter. Vi ønsker så å besvare hvilken pris dette gir, og hva resultatet ved denne tilpasningen er. For å komme frem til prisen, dividerer vi totalinntektsfunksjonen på x, ettersom vi da kommer frem til stykkprisen. Dette henger sammen med at inntektsfunksjonen naturligvis er et produkt av pris og antall solgte enheter. Prisfunksjonen blir dermed:

Bestemmelse av prisfunksjon. Prisen bestemmes som forholdet mellom totalinntekt (TI) og antall solgte enheter. Enten man benytter en salgsinntekt i kroner eller en inntektsfunksjon, gjelder sammenhengen.

Vi bestemmer så prisen ved tilpasningen vi har bestemt, ved å sette inn løsningen som x-verdien i prisfunksjonen.

Beregning av pris ved bruk av prisfunksjon.

Dermed har vi konkludert med at vinningsoptimal mengde er 175 enheter, som gir en enhetspris på kr. 4 400 pr. stk.

Det siste spørsmålet vi ønsker å besvare, er hvilken samlet fortjeneste denne tilpasningen medfører. Vi tar da utgangspunkt i profittfunksjonen, slik den ble beregnet over. Vi kommer da frem til:

Beregning av profitt ved bruk av profittfunksjon.

Dermed har vi konkludert med at ved vinningsoptimal tilpasning, oppnår vi en fortjeneste på kr. 206 250 ved å produsere og selge 175 enheter, som selges til en stykkpris på kr. 4 400.